NEWS ROOM
2022.11.29
POKER ROOMが挑戦する競技ポーカー「TIERレーティング」の仕組みと設計思想
こんにちは、株式会社POKER ROOM開発チームです。この度、ROOTS REWARDS Season.2にて導入されたポーカー向けの新たなレーティングシステム「TIERレーティング」に関して、その中身をシステム的な側面から説明する機会をいただきましたので、ここに公開させていただきます。

この文章では、TIERレーティングがどのような要素で構成されているか、内部の計算がどのようなロジックで行われているのかについて、公開可能な範囲で説明しています。また、運用されるまでにシミュレーションされた計算結果を掲載し、実際にTIERレートの体験がどのようなものとなるかについて直感的に理解できるような解説をしています。
専門的な解説が続く箇所がございますので、まとめの章に要点のみ著しております。なお、TIERレーティングが導入された背景や意図については、POKER ROOM TIERディレクター・横澤真人がディレクターノートに執筆しておりますので、そちらをご一読いただけますと幸いです。
背景
対戦型ゲームにおける最も著名なレーティングシステムとしてEloレーティングと呼ばれるものがある。
Eloレーティングとは、対戦のたびに対戦相手のレーティングに基づいて期待勝率を割り出し、実際の結果に応じてレーティングを決定する手法であり、これによって自身のスキルがレーティングの値となって可視化される。
このEloレーティングは、1900年代半ば頃から国際チェス連盟の公式記録や対戦型オンラインゲームでのランキングなどで幅広く活用されており、現在最も実績のあるレーティングシステムとして知られている。
他にもe-Sportsの世界でよく用いられているGlickoレーティングや、Eloレーティングを拡張させて多人数対戦におけるレーティングに対応させたTrueSkillなど、さまざまなレーティングシステムが存在する。
こういったレーティングシステムは、プレイヤーの現実的な実力を相対的なレートで表現することを目的としており、実力が可視化されることによる競争性の誘発や上位プレイヤーに対する興味関心の喚起、同じ実力同士のプレイヤーとのマッチングなどを機能として持つ。
これらの機能は前述のチェスやe-Sportsにおいて、競技性をより高めるための一助となっていることは言うまでもなく、TIERプロジェクトが目指す【ポーカーの競技シーン】を実現するためにも必要不可欠な要素ではないか、とかねてより着目していた。
しかしながら、1:1の対戦を想定しているEloレーティングやGlickoレーティングなどは、ポーカーのような多人数ゲームにそのまま適用することはできない。さらに、開始から終盤まで参加人数が増減することやプレイヤーによってプレイハンド数にばらつきがあること、またリエントリーによってスタックを復活させることができることなど、ポーカーという多分に特殊な要素を含んだゲームだとなおさら適用が難しくなってくる。
そこで我々は、前述の多人数型レーティングにおいて実績のあるマイクロソフト社が開発したTrueSkill(™)の手法に注目し、これをポーカーにおけるレーティングに応用できないかと考えた。TrueSkill(™)におけるプレイヤーのスキルを確率分布と捉える考え方や、ベイズ確率およびメッセージパッシングなどの数学を応用したシステムをベースに、ポーカー特有の要素をどのようにロジックに組み込むかという試行錯誤と多くのシミュレーションを経て、今回ご紹介するポーカーに特化したレーティングシステム「TIERレーティング」を導入するに至った。
TIERレーティングの概要
前述の通り、TIERレーティングはTrueSkill(™): A Bayesian Skill Rating Systemを参考にシステムが構築されている。ここではその概要と、TIERレーティングで取り入れているポーカー特有の要素について説明したい。
スキルの捉え方
まずはじめに、プレイヤーのスキルが平均値(代表値) および分散 をとる正規分布で表されると仮定する。
正規分布とは、データが平均値付近に左右対称で集積するような確率分布のことで、統計学の分野などでよく用いられる。正規分布に従う分布は自然界に多く存在するとされており、例えば、コインを1000回投げるという試行を10億セット試した時の表が出た回数の分布は、500回を平均値として正規分布に従う。
スキルについても上記のコインを投げる試行と類似しており、試行回数を重ねるとその人が持つ平均的なスキルを発揮する回数が最も多くなるであろうが、調子が悪い時は本来持っているよりも低いスキルを発揮することがあるし、その逆もまた然りである。このような特徴をもとに、プレイヤーのスキルが正規分布に従うと仮定した。
以下、そのプレイヤーのスキルの平均値を として山の中央値で表し、そのばらつきの程度を分散 として表現する。
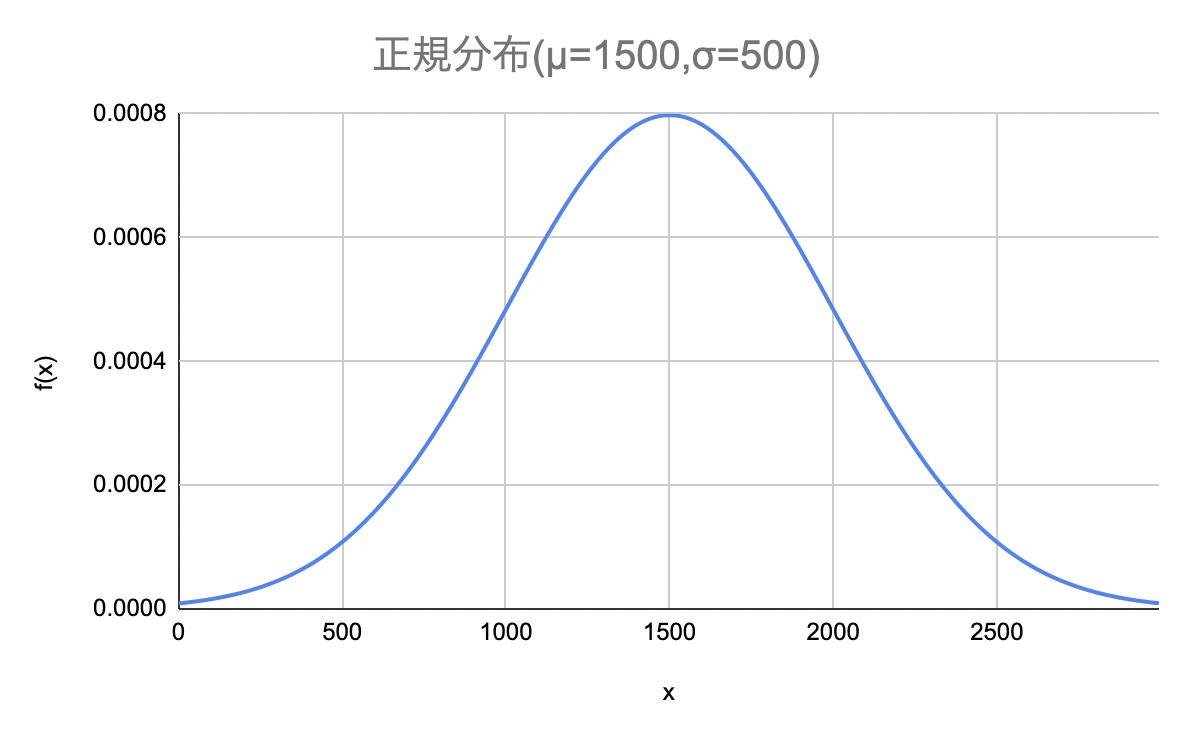
図1: となる正規分布のグラフ
数学的な解釈を補足すると、正規分布の性質から、あるプレイヤーのスキルが から 離れた領域の間にいる確率は約68.2%、 分離れた領域の間にいる確率は約95.4%ということを示している。
この確率分布はプレイヤーごとに異なる分布をとり、対戦回数を重ねるごとに常に変化していく。例えば、勝ち続けると図2の赤線のような分布(トーナメントに15回参加した例)に変化し、負け続けると黄線のような分布(トーナメントに5回参加した例)に変動する。
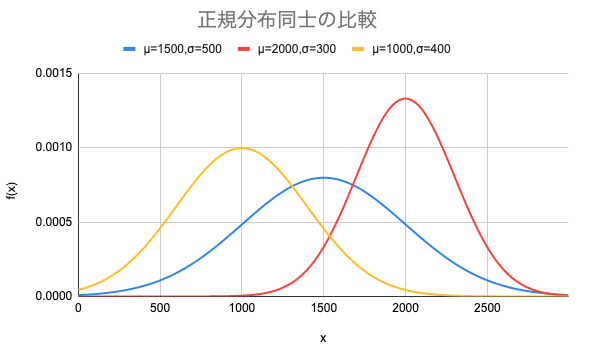
図2: 3種類の異なる平均値および分散をとる正規分布同士の比較
プレイヤーの実力がわからない初期の段階では、ある初期分布を仮定する必要があるが、TIERレーティングではこれを をとるとした(図2における青線)。この初期分布は先ほど述べた正規分布の性質から、あなたのスキル値が1000〜2000の間に存在する確率が約68.2%、500〜2500の間に存在する確率が約95.4%あるということを示している。
の値は分散を表すことから分かるように、基本的には対戦回数を重ねるごとに値が減少していく。例えば、同じ の値をとるとしても、対戦回数を重ねて まで収束していれば、あなたのスキル値は1200〜1800である可能性が高いと表現されることになる。
つまり、プレイヤーのスキルを確率分布で表現するということは、「大体この程度であろう」というスキル値( )とその信頼度( )の2つの要素でスキルを定義するということである。
TIERレートの定義
上記に説明した方法でプレイヤーのスキルを解釈するが、スキル=確率分布と言われてもプレイヤーにとっていまいち直感的ではない。
そこで、TIERレーティングではプレイヤーの実力を「TIERレート」と称し、確率分布ではなくある単一の値で表現することにする。
K: 上側確率が80%となるような定数値(K=0.84162123357)
L: 3回対戦した時点でのTIERレートの中央値が1500となるように調整するための定数補正項
平均値 を基準として、左側に の定数倍だけずらした点をTIERレートと定義した(※ は定数補正項であるため説明において無視している)。数字のみだとわかりづらいが、図で表現すると下図3のように捉えられる。
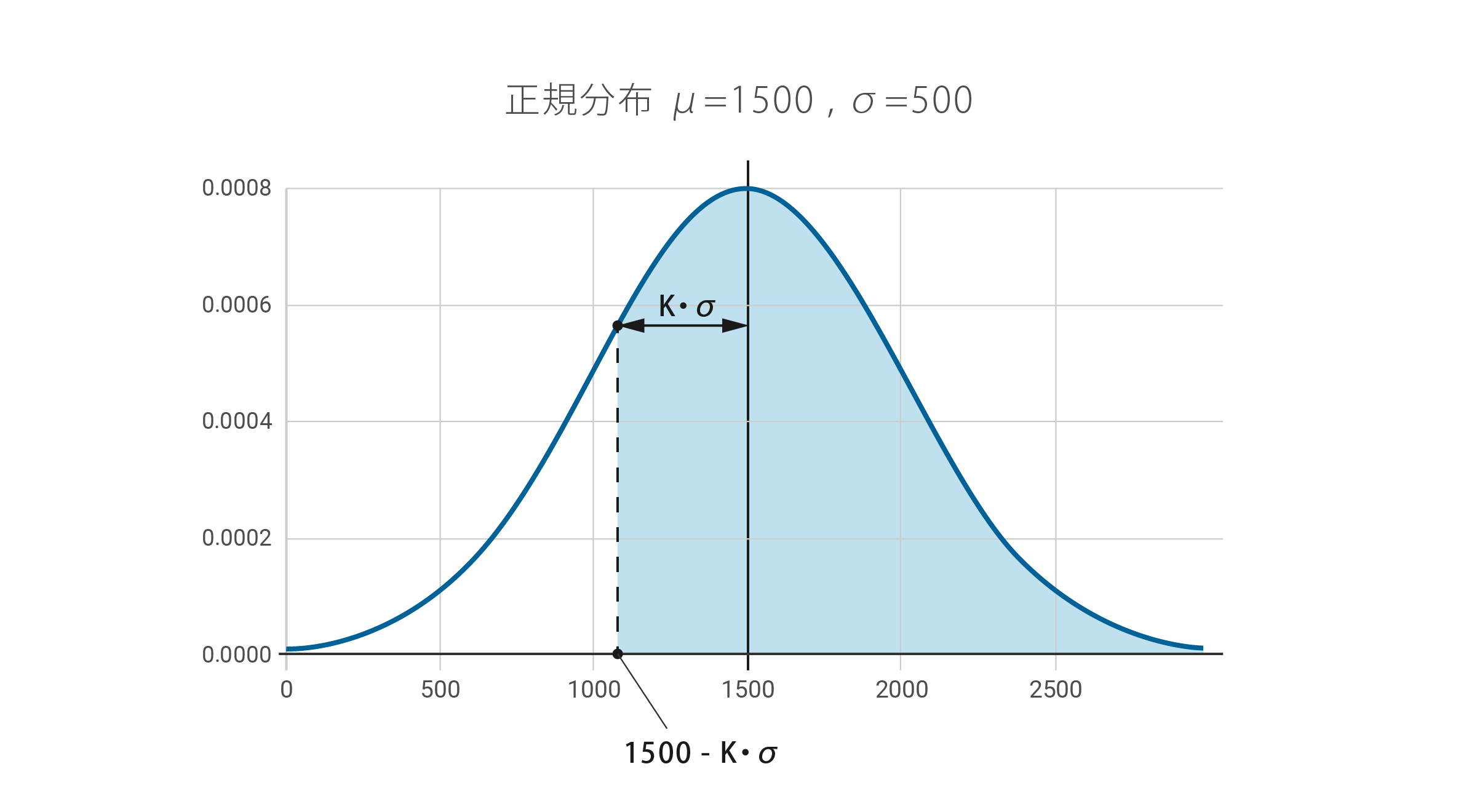
図3: 正規分布上におけるTIERレートの値
ここで としているが、これは正規分布において上側確率が80%となるような値( に関して の点から正の無限大まで積分値をとると0.8となるような値)である。
つまりTIERレートの値は、対象のプレイヤーが持ちうるスキルのうち、上位80%のスキルが発揮されると仮定した時のスキル下限値ということである。別の言い方をすると、プレイヤーの実力を少し控えめに見積もった値であり、「プレイヤーの実力の最低保証ライン」 であるとも言える。
プレイヤーのスキルに関する初期分布は をとるとしたが、この時のTIERレートの値は、定義から分かるように1500から比較的大きくマイナス方向にずれた値となる。一方で、同じ の値を持っていたとしても、参加回数を重ねて が小さくなると、TIERレートの値は初期値よりも大きい値となる。
これはつまり、プレイヤーが参加回数を重ねるごとに、そのプレイヤーのスキル平均値 の値がより信頼できると解釈されるということであり、その結果「プレイヤーの実力の最低保証ライン」であるTIERレートはより高い値として評価されることになる。
TIERレートの更新
以下では、TIERレーティングの根幹部分であるTIERレートがどのようなロジックで更新されていくのかを説明する。なお、機密情報秘匿のため一部ロジックについて非公開としている箇所があることをご了承いただきたい。
a. コア部分
TIERレートは、TIER MATCHに参加するたびに更新されていく。その更新方法についてベースとなる手法は、以下の通りである。
まず、プレイヤーがトーナメントに参加する前のスキルを事前確率分布、トーナメントの結果を観測値として得られるスキルを事後確率分布とするようなベイズ確率の考え方を用いて、TIERレートを更新することを考える。
TrueSkill(™)では1つの対戦におけるプレイヤーのスキル分布と対戦結果の関連性を図4のようなファクターグラフで表現しており、TIERレーティングでもこれに従う。
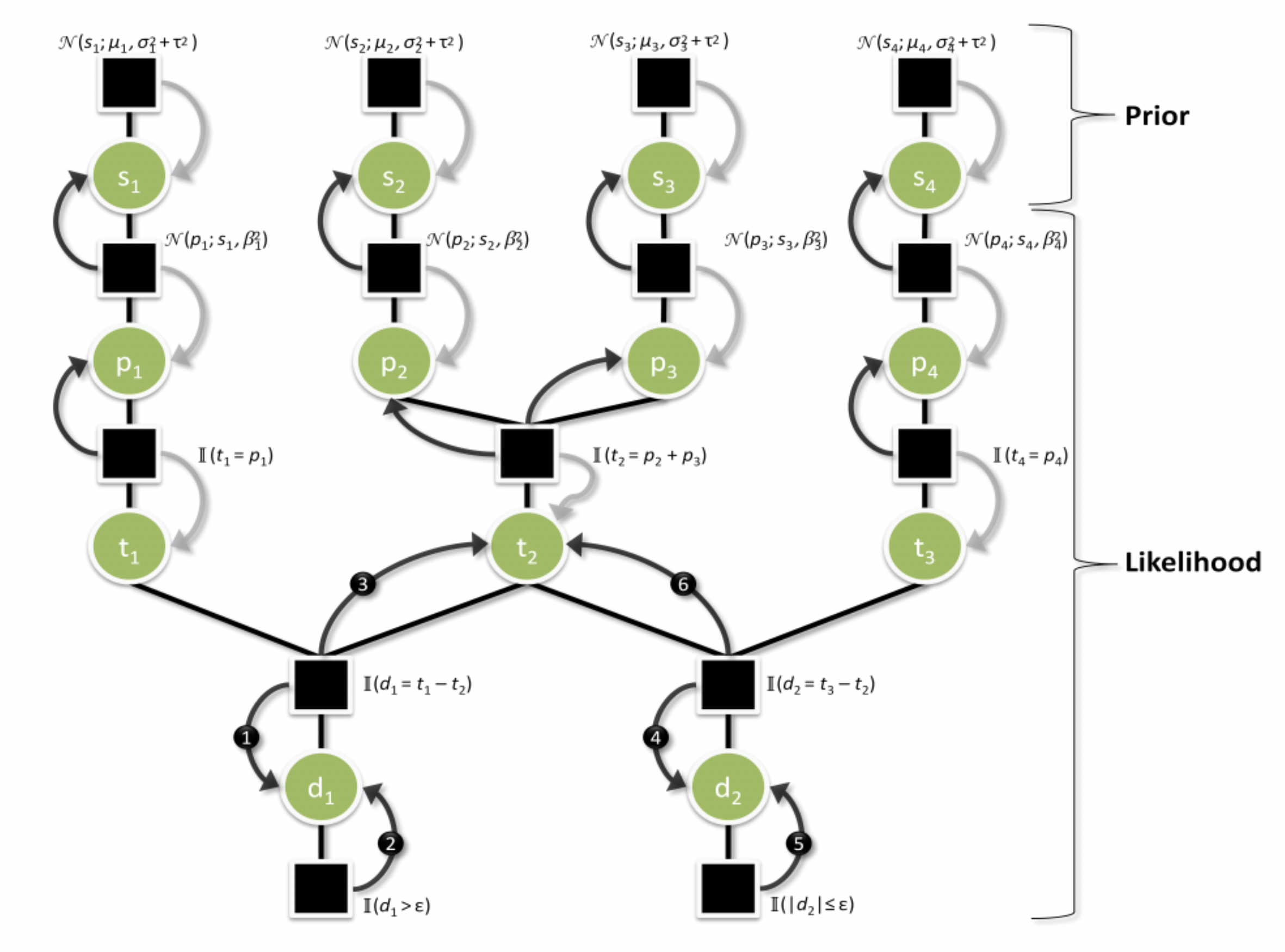
図4: 多人数対戦におけるグラフィカルモデル(ファクターグラフ)(引用元:The Math Behind TrueSkill)
: 各プレイヤーに割り振られたインデックス
: プレイヤーのスキルを表す確率変数ノード
: トーナメントにおけるパフォーマンスを表す確率変数ノード
: チーム戦を考えた時のチームパフォーマンスを表す確率変数ノード ※執筆時点でのTIER MATCHにおいてチーム戦は存在しないため、現時点では ノードとイコールになる
: 各プレイヤー間で対戦した時のパフォーマンスの差を表す確率変数ノード
■: 接続された確率変数ノードに関連する関数
: 平均値 , 分散 をとる正規分布を とする
: 定義関数
このモデリングでは、プレイヤーのスキルとトーナメント結果が依存関係にあり、プレイヤー間の実力の差がトーナメント結果に差分として現れるという直感的にも理解できる関係性をモデル化している。
ただしこのファクターグラフ表現は、単に複数対戦をモデル化することだけを目的としているのではなく、各丸ノードに表現した周辺確率と四角ノードで表現した丸ノードに関連する関数群同士を、メッセージパッシングと呼ばれる手法を用いて簡易的かつ効率的に計算することを主目的としている。
実際の計算順序としては、まず にトーナメント参加前のレートを事前確率分布として与え、トーナメントの結果である順位を観測値として ノードにセットし、 ノードまでメッセージパッシングを行う(図4の灰色の矢印)。その後チームパフォーマンスの差を表すノードの周辺において、図4の黒矢印①〜⑥に示すような順番でメッセージパッシングを繰り返し行う。最後に図4において番号を振っていない黒矢印に示すような方向にメッセージパッシングを行い、最終的に更新された の確率分布を事後確率分布として計算を終了する。
つまり、対戦前の各プレイヤーのスキル値から発揮されるパフォーマンスを予測しておき、実際のトーナメント結果がその予測からどれだけずれていたかを計算し、その結果を元にトーナメント終了後の各プレイヤーのスキル値をより適切な値に更新するということを行っている。
ここでは高級概念の説明に焦点を当てているため具体的な計算式は割愛しているが、より詳細な説明やメッセージパッシングで用いられる計算式、各種定義された関数群などについて知りたい方は、TrueSkill(™): A Bayesian Skill Rating SystemまたはThe Math Behind TrueSkillが詳しいため、そちらを参照していただきたい。
b. スキルとパフォーマンスの相関関係を決定する
スキルとパフォーマンスの相関関係というのは、a. のファクターグラフで示したところの のことである。このうちスキル値の分散として定義されている は、プレイヤーが持っているスキルがどの程度のばらつきを伴ってパフォーマンス(トーナメントにおける順位)として発揮されるかを表している。
つまり、 が大きければ大きいほど偶然性の高いゲームであることを表し、 が小さければ小さいほどスキルの差が顕著に現れるゲームであることを表しているといえる。一般的なスキルゲームにおいて、 で設定される時の の値には が使われることが多いようであるが、ポーカーという偶然性の高いゲームを扱うTIERレーティングでは、これを とした。
また、The Math Behind TrueSkillの説明を引用すると、スキル連鎖という考え方を用いて の値に対する理解を深めることができる。上記によると、スキル連鎖は下図のように、左端の最も成績の悪いプレイヤーと右端の最も強いプレイヤーで構成され、両端のプレイヤーに続くプレイヤーは、そのプレイヤーよりも だけ離れたスキルを持つプレイヤー( だけ離れたプレイヤー同士の勝率は約20%:80%になる)を一列に繋げて構成されると表現されている。
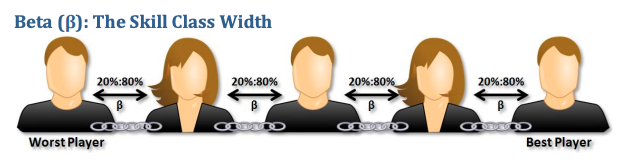
図5: βによるスキル連鎖(引用元:The Math Behind TrueSkill)
スキル連鎖を考えると、 の大きさによってプレイヤー全体のスキルがどの程度ばらつくのかを数値感覚として捉えることができる。
例えば、図における「Worst Player」のスキルを仮に1000、「Best Player」のスキルを3000とした時、TIERレーティングでは であるため、この両者の間に一人だけプレイヤーがいるようなスキル連鎖となる。これを例えば とした場合は、両者の間には勝率が20%:80%ずつ離れたプレイヤーが7人いることになり、ポーカーにおけるスキル連鎖としては適切でない。
ポーカーにおいて、プレイヤー同士の勝率が20%:80%になるケースは考え難いが、試行回数が限られた環境での下振れや上振れ、プレイヤーの相性(より広義で言うとエクスプロイト戦略=最適反応によって利得が最大化されうる状況)による偏り、また1:1だけではなく多人数対戦を含めて考えた時の勝率のことを指すことなどを考えればあり得なくはないだろう。
先ほども述べた通り、TIERレーティングでは の値を1000としたが、この値は各シーズンにおける実績を踏まえ、より実力に即したレートを算出することを目的に今後アップデートされる可能性がある。なお、アップデートのタイミングについては、シーズンの切り替わり時を想定している。
c. レジストクローズ前にBUSTしたプレイヤーへの対処
最終的に全体のエントリー数が100人となるトーナメントにおいて、まだ20人しか参加していない状態で1番最初に飛んでしまったプレイヤーがいた状況を考える。
そのプレイヤーがBUSTした時点では20/20という順位だったはずが、トーナメントが終了した時点での順位は100/100となってしまう。ここでa.に述べた方法でレート計算を行うとすると、最終順位である100/100という結果を元にレートが算出されるが、それだと後から参加したプレイヤー数が多ければ多いほど早期にBUSTしたプレイヤーが損をするような構造になってしまう。
そのためTIERレーティングでは、a.で説明したレーティング計算をプレイヤーがBUSTした時点におけるプレイヤープールを元に行う手法をとることにした。以下、これを"部分ゲームにおけるレーティング"と呼ぶことにする。
つまり部分ゲームにおけるプレイヤーについてのレーティング計算では、対象のプレイヤーと、そのプレイヤーがBUSTした時点において残っているプレイヤー、およびその時点でBUSTしてるプレイヤーをプレイヤープールとして順位を仮決定し、その集合を元にファクターグラフを定義して、aと同様の計算を行い対象プレイヤーの事後スキル分布を算出する。これを、部分ゲームをプレイした全プレイヤー(レイトレジスト前にBUSTしたプレイヤー)に対して行う。ここで、対象のプレイヤーがBUSTした時点において残っているプレイヤーの順位については、最終順位の順序に従うものとする。
このような方式で部分ゲームにおけるレーティングを行うことで、レート計算が自分がプレイしたフィールドに対してのみ行われ、自分がBUSTした後に参加したプレイヤーがいたとしても、自分の獲得レートが影響を受けることはなくなる。
d. 先にBUSTしたプレイヤーがいる場合にレジストしたプレイヤーへの対処(一部ロジック非公開)
これはいわゆるレイトレジストのことである。c.では自分がBUSTした後にレイトレジストしたプレイヤーがいた場合に、自分が不利にならないようなロジックを組み込んだが、逆にレイトレジストしたプレイヤーは、既にBUSTしてるプレイヤーの分だけ(マイナスを避けられるという意味で)得をする構造のままである。そのため何らかの下方修正を受ける必要がある。
これにはさまざまな方法が考えられるが、TIERレーティングでは、①部分ゲームおよび全体ゲームのそれぞれにおいて各プレイヤーが獲得するTIERレートの合計値の差分に着目し、これと②ICM(Independent Chip Model)の考え方を組み合わせてレイトレジストしたプレイヤーに対する補正をかけている。具体的なロジックについては非公開とさせていただくが、それぞれの概要について以下に説明する。
①部分ゲームによるレーティングを導入しなかった場合に計算された各プレイヤーiのTIERレート変動値を 、部分ゲームによるレーティングで計算された各プレイヤー のTIERレート変動値を とすると、常に が成り立ち、その和についても が成り立つ。この差分はプレイヤー よりも後に参加したプレイヤー、つまりレイトレジストしたプレイヤーによって発生しており、これをレイトレジストしたプレイヤーに対する補正値として導入する。
仮に補正値の度合いを とした時に、レイトレジストしたプレイヤー が参加した時における全体エントリー数を 、同タイミングにおいて既にBUSTしてるプレイヤーの人数を とすると、
※~は左辺と右辺が比例関係にあることを表す
と表せるような値Cを補正値とする。
②一般的にICMとは、トーナメントにおいて各プレイヤーの賞金期待値を計算するシステムのことを指し、全体のスタック と各プレイヤー のスタック の比率 をそのプレイヤーの優勝確率とする考え方をベースに計算される。エントリー数を 、 をプレイヤー がとりうる順位の確率変数として、プレイヤー が 位をとる確率は以下のように表せる。
ここで とした。
さらに、ICMでいう賞金の部分を獲得TIERレートに置き換えて、プレイヤー が 位をとった場合の獲得TIERレートを 、プレイヤーが参加した時点における残り人数を とした時の獲得TIERレート期待値 を考えることができる。
任意のプレイヤーが1人以上BUSTした状態のトーナメントにおいて、プレイヤーiがレイトレジストした場合の獲得TIERレート期待値 は、そのプレイヤーがトーナメント開始直後から参加していた場合の獲得TIERレート期待値 よりも大きくなる。
レイトレジストしたプレイヤーはICMの観点からみるとこの差である 分得をすることになるため、これを①と合わせてレイトレジストしたプレイヤーの補正値として導入する。
これら①②を合わせた補正をレイトレジスト補正 とするが、このまま適用するとレイトレジストしたプレイヤーは損も得もしない状態をつくることになるため、実際にはこの値から25%増しの値をレイトレジスト補正値 とする。
これによってレイトレジストしたプレイヤーは、そうでないプレイヤーに比べて常に損をすることになる。また、エントリーが遅ければ遅いほど(正確にはエントリーした時点で先にBUSTしたプレイヤーの割合が多ければ多いほど) の値は大きくなるため、レイトレジストによって受ける損分も大きくなる。
なお、リエントリーしたプレイヤーに関しては、上記で算出した の値をそのまま補正値として適用することにする。リエントリーの場合、ファーストエントリーとは違い、プレイヤーは常にトーナメントの序盤から参加することができないという制約がある。これによってプレイヤーはレイトレジストを強制され、TIERレートの観点から損をする状況に置かれるため、場合によってはリエントリーをしないことがTIERを上げていく上で適切な戦略となってしまう場合がある。
しかしながら、本来プレイするはずだったトーナメントの機会を、TIERレートの観点で損をするからという理由で奪ってしまうのは本意ではない。ましてや限られた回数しか参加できないライブトーナメントにおいては尚更である。
上記のような、TIERレーティングの仕組み自体がポーカーをプレイする機会を減らしてしまう状況をなるべく避けたいため、リエントリーをした場合においてのみレイトレジストが損でも得でもなくなるような方式をとることにした。
e. ハンド数について(一部ロジック非公開)
一般的な対戦ゲームではそれぞれのプレイヤーのプレイ時間が同じになることがほとんどであるが、ポーカーではレイトレジストが可能なことによって、プレイ時間(≒ポーカーに置き換えるならハンド数)にばらつきがある。たとえ結果的に同じ順位であっても、ハンド数が少なければ少ないほど、その結果に対する重要度は相対的に低くなるべきであるため、その要素をレーティングに取り入れたい。そこでTIERレーティングでは、ハンド数が少ないほど相対的にレート変動率が小さくなるようなロジックを組み込むことにした。
ハンド数を表現するための指標は、プレイ時間や1テーブルあたりの平均プレイ人数、ストラクチャーの違い、1プレイあたりかかる平均的な時間などさまざまあるが、TIERレーティングでは、ハンド数指標が以下の式に従うものとする。
ハンド数指標( ) = プレイ時間( ) 単位時間あたりハンド数指標( )
※実際のハンド数ではなくハンド数を表す指標としている点に注意
さらに、 は1テーブルあたりの最大人数( )に依存するものとする。例えば、9maxのトーナメントであれば は比較的小さくなるし、ヘッズアップであれば大きくなる。 と の依存関係については、トーナメントにおけるテーブル人数ごとの推定 (Voluntarily Put Chips In Pot)をもとに、 の時の を として以下のように定めることにした。
つまり、 を基準にした時の の上昇率を、 の上昇率の50%とするということである。
ここで、 は1テーブルあたりのプレイ人数が最大 人である時の推定VPIPを表しており、プリフロップにおけるハンドレンジから、例えば9MAXでは20.0、2MAX(ヘッズアップ)では80.0を用いる。
また、VPIPの上昇率による寄与分を控えめに設定しているのは、VPIPがそのまま単位時間あたりのハンド数指標になる訳ではないであろうということや、ROOTSで行われるような参加人数が限られたライブトーナメントにおいて、実際のテーブルあたりプレイ人数は よりも(ヘッズアップを除くと)小さくなることがあるということを考慮したためである。
これらをもとに、プレイ時間と1テーブルあたり最大人数の2つを相対的に重要な指標と捉え、ハンド数に関する重み付けを行う。具体的な計算ロジックについては非公開とするが、仮にハンド数にかかるレート変動率に関する重要度を表す指標をHとすると、
で表し、TIERレーティングの計算部分のうちレート変動率を決定するロジックに組み込む。ただし、 には下限値及び上限値が別途設定されており、それを超えて補正がかかることはない。
これらの関数や各種係数についても、各シーズンにおける実績を踏まえて今後アップデートされる可能性がある。
f.リエントリーについて
ここまでに説明した手法を用いて、順位が決まるような多人数対戦においてのレーティングが実現できるが、計算対象のプレイヤーは全て異なることが前提のため、ポーカー特有の要素であるリエントリーを扱うには少し工夫する必要がある。
TIERレーティングでは、上記で説明した計算をエントリー可能回数分繰り返して、リエントリーしたプレイヤーのTIERレートを求めることにしている。
具体的には、 回目の計算で得たプレイヤーの事後レートを、 回目エントリー分の事前レートとしてセットし、 回目の計算を行うことにより、リエントリーしたプレイヤーの事後レートを求める(事前/事後についてはいわゆるベイズ統計などで用いられる事前/事後分布の意味で使っている)。 回目のエントリーをしたプレイヤー における 回目のループでの事前レート、事後レートをそれぞれ 、 、また 回目にリエントリーしていないプレイヤーを とすると、 回のループにおいて、
と表せる。
これにより、リエントリーしたプレイヤーがいた場合は、対象のトーナメントに複数回参加したことと見なし、レーティングを行っている。
別の手法として一度のループで計算した複数エントリー分の事後レートを平均合成する方法も考えられるが、その場合にたとえば、それぞれの順位に大きな乖離があるケースを考えると、事前レートよりも (分散)の値が大きくなることがある。運要素が強いポーカーというゲームにおいてこれは高頻度で発生しうるし、1シーズンという試行回数が限られた短い期間の中では分散を収束させることが難しくなってしまう。
また、TIERレートの定義から、 の値が大きくなることでTIERレートの値は下がる方向に変動してしまうが、これもあまり直感的ではない。
上記のような理由から、TIERレーティングではリエントリーを別々のエントリーとして再計算し、最終的な結果をプレイヤーのレートとするようなロジックを組むことにした。
g. 順位について
海外で開催されているトーナメントでは、通常上位x%だけに賞金が発生し、それ以外のプレイヤーはリターンを得られないため、賞金発生ライン付近ではICMを強く意識してプレイすることができる。
また、一般的にはトップヘビーに賞金の傾斜がかけられることが多く、賞金ジャンプが発生する順位などでもICMを意識すると言うポーカー特有の面白さがある。
TIERレーティングでは、全順位にTIERレートの獲得が発生するため少なからずICMを意識することになるが、よりその要素を強めるために特定順位における獲得TIERレートに重みづけをし、順位ごとに傾斜がかかるようにした。
| 順位 | 重み |
|---|---|
| 1位 | 1.0 |
| 上位3% | 0.97 |
| FT進出者 | 0.95 |
| 下位3% | 0.92 |
| その他の順位 | 0.8~0.9のいずれか |
1位の1.0を基準として上記のような重みによる傾斜をかける。これによって、下記の条件を達成することに重要性が出てくる。
- 1位をとること
- 上位3%に入ること
- FTに進出すること
- 下位3%を抜けること
なおこの傾斜をかける際、"その他の順位"のプレイヤーの重みは、傾斜をかけた後の全プレイヤーの獲得TIERレートの合計値と傾斜をかける前のそれとの差分が0に最も近づくような値を選択し決定している。
またこれらの重み係数についても、各シーズンにおける実績を踏まえて今後アップデートされる可能性があることに留意されたい。
シミュレーション
TIERレーティングのロジックの確からしさを確認するために、強さの異なるプレイヤーを複数人用意し、架空のトーナメントを複数回開催してレートの変動を見るシミュレーションを行った。なお、ディレクターノートにてシミュレーションの結果を一部掲載しているが、その時とシミュレーション条件が異なることに留意されたい。
条件
まず、5種類の強さが異なるプレイヤーを1000人用意する(ここで、全プレイヤーは の初期スキル分布をとる)。
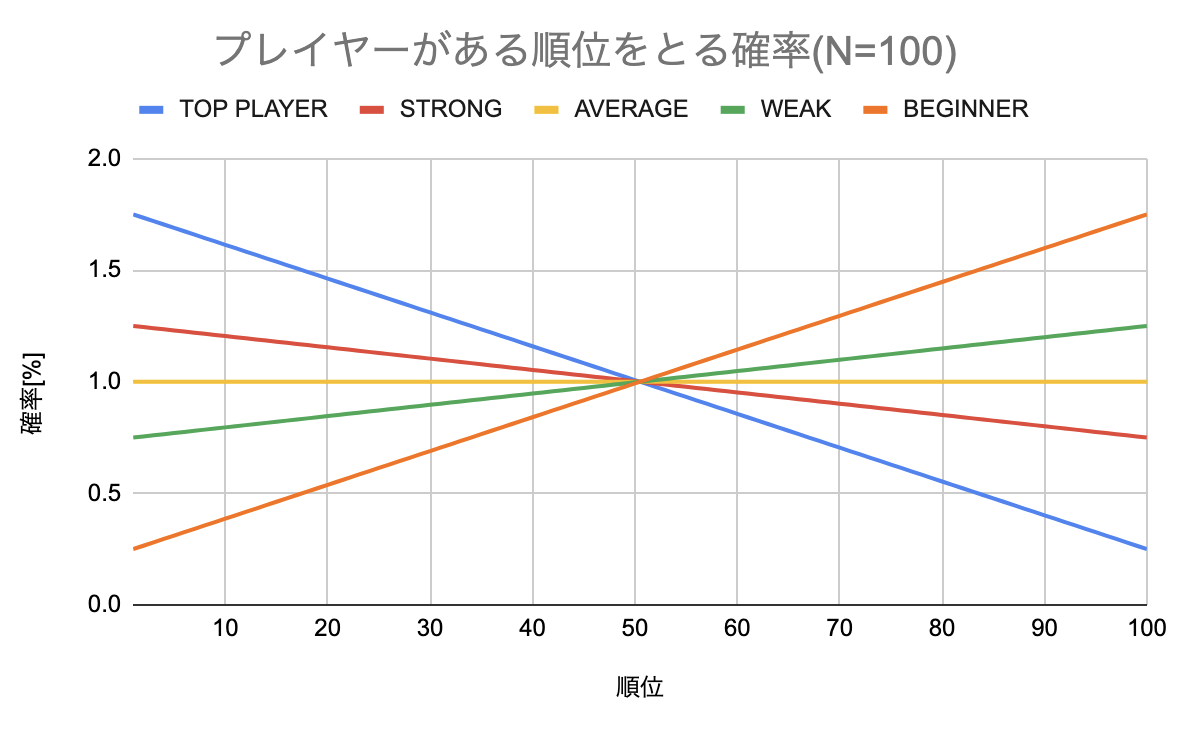
図6: エントリー数100人のトーナメントにおいてプレイヤーがある順位をとる確率
5種類のプレイヤーの定義は図6に示したように、平均的な強さのプレイヤーが1位〜100位までを等しい確率でとるものとして、最も強いプレイヤーだと1位を1.75%、最下位を0.25%の確率でとり、その間の順位は線形的な確率で取るものとする。
つまり、順位を 、その順位をとる確率を確率[%]を とすると、
の式に従ってプレイヤーの順位を決める。
また、それぞれのプレイヤーの数は以下の通りとした。
TOP PLAYER … 1000×0.05 = 50(人)
STRONG … 1000×0.25 = 250(人)
AVERAGE … 1000×0.4 = 400(人)
WEAK … 1000×0.25 = 250(人)
BEGINNER … 1000×0.05 = 50(人)
このプレイヤーの集合から1回あたりに参加するプレイヤーをランダムに抽出し、トーナメントに参加させて順位を決める。開催するトーナメントは、以下の2種類とする。
| トーナメント時間 | 枠数 | 開催回数 | 1テーブルあたり人数 |
|---|---|---|---|
| 300分 | 50 | 250 | 9MAX |
| 600分 | 100 | 75 | 9MAX |
また、全プレイヤーはトーナメントの序盤から参加するものとし、リエントリーはせずトーナメント開始から終了まで間に一定時間おきにBUSTしていくものとする。
これに対して、全てのプレイヤーが最終的に20回ずつ各トーナメントに参加するようなシミュレーションを行った。
強いプレイヤーは最終的に高レートに分布される
下記にシミュレーションを行った後における各プレイヤー種別ごとの平均順位と平均TIERレートをまとめた。なお、ALLは全プレイヤーを指している。
| プレイヤー種別 | 平均順位(分子) | 平均順位(分母) | 平均順位上位% | 平均TIERレート |
|---|---|---|---|---|
| TOP PLAYER | 27.6 | 69.1 | 40.0 | 1939.4 |
| STRONG | 32.2 | 68.7 | 46.8 | 1742.3 |
| AVERAGE | 34.8 | 68.7 | 50.7 | 1621.5 |
| WEAK | 37.4 | 68.8 | 54.4 | 1504.0 |
| BEGINNER | 43.4 | 68.8 | 63.0 | 1238.0 |
| ALL | 35.1 | 68.8 | 50.1 | 1619.0 |
より強いプレイヤーは高確率で高い順位をとるため、平均順位のスコアが良くなることは自明であるが、この時平均TIERレートのスコアも高くなることが分かる。
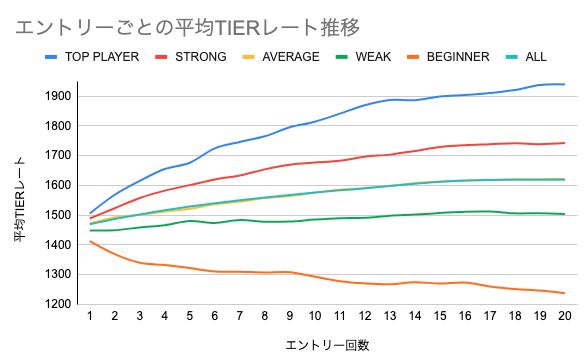
図7: エントリー回数ごとのプレイヤー種類別平均TIERレート推移
図7に、エントリー回数ごとの平均TIERレートがどのように推移するかについて示した。
ALLに注目すると、最終的なTIERレートは1618付近に収束していくことがわかる。これは「TIERレートの定義」でも説明したように、参加回数を重ねると の収束によってTIERレートは上昇するようになっており、 が収束しきった時のTIERレートの平均値が約1618になるからである。
また、ALLの3エントリー目におけるTIERレートに注目すると、ちょうど1500になっていることがわかる。これは後で説明するように、3回エントリー時点におけるTIERレートの中央値が1500になるような設計にしているからである。
この3エントリーというのはROOTSにおいて「振り分け戦」とされている期間であり、σの収束度が全体の30%となる期間として定めている(後に説明するが、σは初期値500からはじまり、3エントリーで440まで収束し、300を下限値としてその後変動しなくなる)。
参加回数とレート変動の関連性
先ほど「15回参加した後におけるTIERレートの中央値が1618になる」ということに触れたが、これはTIERレートの定義から説明できる。
: 上側確率が80%となるような定数値( )
: 3回対戦した時点でのTIERレートの中央値が1500となるように調整するための定数補正項
ここで定数補正項 について説明する必要があるが、これは3回対戦した時点でのTIERレート中央値が1500になるように設定している。
3回対戦した時点での の中央値をそれぞれ 、 とすると、
※3回エントリーするシミュレーションを繰り返すことによって得られた平均値
となる。これを3回対戦した時点でのTIERレート中央値が1500であることを使って定義式に代入すると、
となり、 の値は 、つまり と求まる。これを用いて15回参加時点でのTIERレート中央値を求めると、
となる。
※ここで15回エントリーするシミュレーションを繰り返すことによって得られた平均値 を用いている。
各対戦において、 の値は0に収束する方向に変動するため、TIERレートの中央値は対戦を重ねるごとに高くなっていくことになる。図8にその様子を示した。
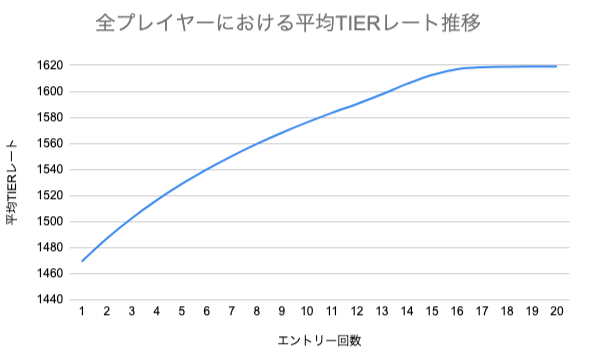
図8: エントリー回数ごとの平均TIERレート推移
最初に説明したように、TIERレートはそのプレイヤーの実力の平均値に加えて、その値がどれだけ信頼できる値なのかを数値にした指標だと捉えられるため、 が収束することによるTIERレートの増分は、プレイヤーのレートがより信頼できる値になったことの程度が反映されたものだと考えることができる。
この の値は通常0に向かって収束していくが、TIERレーティングでは、 はある一定まで下がるとそこから変動しなくなるような閾値(これが という値で、約15エントリーで到達する)を設けている。これには、単純に参加回数を増やせば良いという構造にならないようにする狙いと、収束しすぎないことによってどのレート帯のプレイヤーもある一定のレート変動によるダイナミクスを体験できるというゲーム性を担保したいという狙いがある。
TIERの決定
ROOTS REWARDS Season.2では、Season.1で運用していたTIER POINT(TP)制度を廃止し、TIERレートによってTIERが決まるという全く新しいシステムに生まれ変わる。システムの変更に伴って、それまで7分類であったTIERを10分類まで増やし、新しくTIER AⅢ〜AI、Sを追加した。
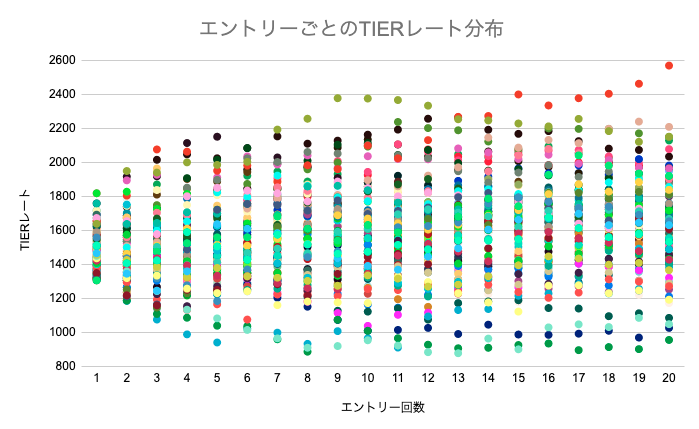
図9: エントリー回数ごとのTIERレート分布
シミュレーションにより、エントリーi回目時点におけるTIERレート分布は図9のような推移になることがわかっている。1回目時点では1500周辺に密集しており、3回目時点から広く分布し始め、5〜10回目で上限下限が決まってくるような推移になることがわかる。
TIERは10分類されるため、ベースとしては各ランク帯に全体の10%程度のプレイヤーが分類されるような閾値を設定しつつ、15回エントリー時点で最も分布が多い領域に中間位のTIERを設定するようにした。また、最上位であるTIER Sには、3回エントリー時点で1〜3%程度のプレイヤーが到達できるような閾値に設定することにし、最終的には全体の5%程度がTIER Sに分類されることを想定している。
| TIERレート | TIER |
|---|---|
| 2000〜 | S |
| 1900〜1999 | AI |
| 1800〜1899 | AⅡ |
| 1700〜1799 | AⅢ |
| 1600〜1699 | BI |
| 1500〜1599 | BⅡ |
| 1400〜1499 | BⅢ |
| 1300〜1399 | CI |
| 1200〜1299 | CⅡ |
| 〜1199 ※900が下限値 | CⅢ |
図10に、全プレイヤーがi回目のエントリーを行った時点におけるTIER分布がどのように変化していくかを示した。この図からも、序盤から終盤にかけて中間位のTIERを中心に全体が分布し、より上位/下位のTIERにいくに連れてその割合が少なくなっていることがわかる。
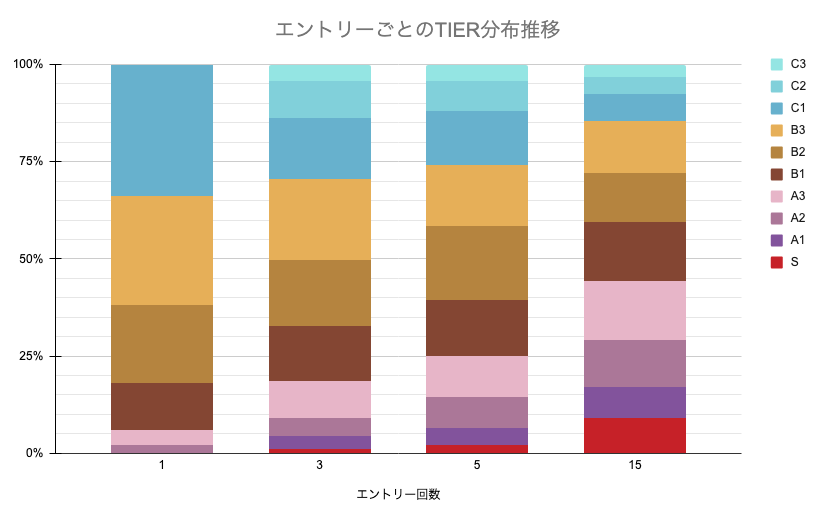
図10: エントリーごとのTIER分布推移
また、シミュレーションの対象である5種類のプレイヤーについて、トーナメントに15回エントリーした時点におけるTIER分布は以下の通りとなった。
| TIER S | TIER A | TIER B | TIER C | |
|---|---|---|---|---|
| TOP PLAYER | 48.0% | 42.0% | 10.0% | 0% |
| STRONG | 14.0% | 53.2% | 28.0% | 4.8% |
| AVERAGE | 5.2% | 41.3% | 44.0% | 9.5% |
| WEAK | 0.4% | 20.4% | 58.4% | 20.8% |
| BEGINNER | 0% | 2.0% | 28.0% | 70.0% |
この分布からわかるように、上位順位を高確率で取るようなTOP PLAYERの多くはTIER S/A帯に分類され、下位TIER帯にはほとんど分類されない。また、平均的な実力を持ったプレイヤーでも、最上位であるTIER Sに到達することがかなり難しいことや、平均以下の実力を持ったプレイヤーは、上位TIER帯に入ることに壁があることがわかる。
この結果は、TIERレーティングによるTIER分類が高確率で実力に即したものになっていることを示しており、15エントリーという比較的短い試行回数で達成されるというのは特徴的である。
エントリーごとのTIERレート変動率について
トーナメントに1回参加するごとにどの程度レートは変動するのだろうか。
これに関しては、そのプレイヤーおよび他参加プレイヤーのTIERレートや分散( )値、トーナメントのエントリー人数、最終順位、プレイ時間、どのプレイヤーがどの順番で飛んだか、などさまざまな要素が関係するため一概には言えないが、たとえば分散値が高い参加回数3回以下のプレイヤーが1位/100人を取ると約+200〜+400程度変動する。しかし、これがたとえば同じ順位でも分散値が低い状態では+100〜+200程度になったり、プレイ時間が短かったりすると、より変動が小さくなる。
図11〜13に、シミュレーションにより出したTIERレート推移を3プレイヤー分載せておくが、あくまで参考値として捉えていただき、実際のトーナメント状況により大きく変わり得ることを念頭に置いてもらいたい。なお、グラフの各点におけるラベルは順位を表し、分母表示しているラベルはエントリー数を示す。
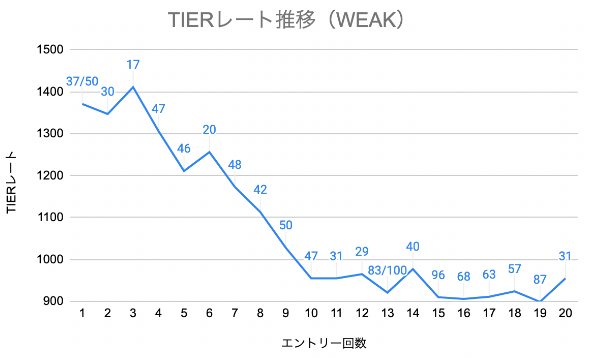
図11: WEAKの中で比較的悪い成績を納めたプレイヤーの順位およびTIERレート推移
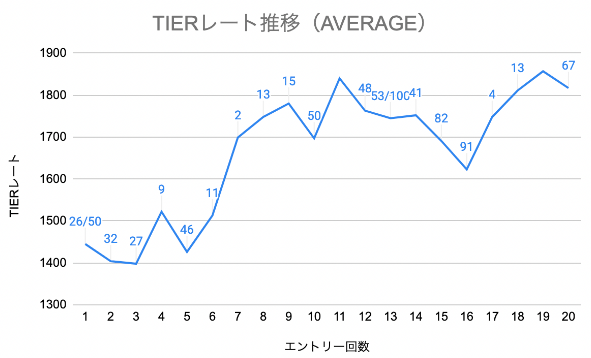
図12: AVERAGEの中で比較的好成績を納めたプレイヤーの順位およびTIERレート推移
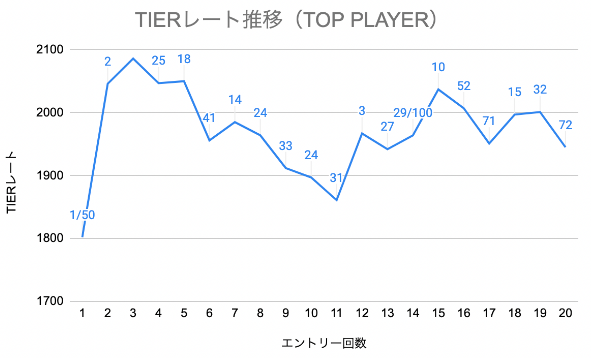
図13: TOP PLAYERの中で平均的な成績を納めたプレイヤーの順位およびTIERレート推移
フィールドの強さとレーティング変動の関連性
全体がレート2000のフィールドでレート1500のプレイヤーが勝つ方が、全体がレート1500のフィールドで勝つよりも変動率は大きい。図14に先ほどTIERレート推移を示したTOP PLAYERと全く同じシミュレーションを、他プレイヤーのTIERレートが全員2000になるように設定して行った結果を示す。
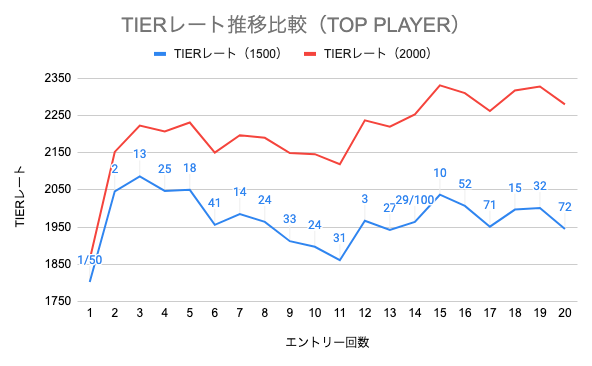
図14: TOP PLAYERのTIERレート推移比較(他プレイヤーのTIERレートを2000に固定)
赤の折れ線が他プレイヤーのTIERレートを2000に固定した時の推移であるが、TIERレートを2000に固定しないシミュレーションを行った時の推移と比較して、TIERレートが上がりやすく、また下がりにくくなっていることがわかる。このように、フィールドに自分よりも強いプレイヤーが多ければ多いほど、勝利した時のレート変動は大きくなり、負けた時のレート変動は小さくなる。
より一般化して、TIERレートが高いプレイヤー と低いプレイヤー が対戦した時、前者のTIERレートを 、後者のTIERレートを として、TIERレート変動率について次のことがいえる。
| が大きい | が小さい | |
|---|---|---|
| が に勝利した時 | TIERレート変動率はかなり小さい | TIERレート変動率は比較的小さい |
| が に勝利した時 | TIERレート変動率はかなり大きい | TIERレート変動率は比較的大きい |
つまり、TIERレートが離れていればいるほど、対戦結果が想定通りであればTIERレートの変動率は小さく、想定通りでなければ大きいということになる。
先ほどの例では、自分のTIERレートだけ1500、自分以外全てのプレイヤーがレート2000という が大きい設定であったため、そのフィールドで勝ち続けることにより最終的なTIERレートは高くなった。ただし、かなり極端な設定のため、実際に起こりうるケースのほとんどはこれよりも緩やかな変化になるであろう。
レイトレジストによる補正影響
ここまでのシミュレーションは、全プレイヤーがレイトレジストをしないという条件で行ったが、最後にレイトレジストによる補正影響について示したい。
参加タイミング以外の条件はそのままにして、レイトレジストに関する条件を下記のように設定し、シミュレーションを行った。
- 半数のプレイヤーは、トーナメントが開始された直後にエントリーする
- 残り半数のプレイヤーは、レジストクローズまでの間に一定時間おきにエントリーする
以下の表に、シミュレーションを行った後におけるプレイヤー種別ごとの平均TIERレートを、レイトレジストあり/なしで比較した結果を示す。
| レイトレジストなし | レイトレジストあり | 差分 | |
|---|---|---|---|
| TOP PLAYER | 1939.4 | 1821.2 | -118.2 |
| STRONG | 1742.3 | 1632.2 | -110.1 |
| AVERAGE | 1621.5 | 1562.8 | -58.7 |
| WEAK | 1504.0 | 1455.5 | -48.5 |
| BEGINNER | 1238.0 | 1182.6 | -55.4 |
ここからわかるように、20回エントリーしたプレイヤーは、一定の割合でレイトレジストをすることによって合計50〜120程度のペナルティを受けることになる。
なお、平均TIERレートについて弱いプレイヤーの方の差分が小さくなるのは、よりトーナメント序盤でBUSTするプレイヤーという設定のため、そもそもレイトレジスト自体トーナメント序盤で行っている割合が高いためである。
また、各プレイヤー種別ごとのTIER分布は以下のようになった。
| TIER S | TIER A | TIER B | TIER C | |
|---|---|---|---|---|
| TOP PLAYER | 8.0% | 70.0% | 22.0% | 0% |
| STRONG | 2.4% | 31.6% | 56.4% | 9.6% |
| AVERAGE | 1.0% | 19.5% | 60.2% | 19.3% |
| WEAK | 0.4% | 8.0% | 54.4% | 37.2% |
| BEGINNER | 0% | 0% | 4.0% | 96.0% |
これらより、常時一定の割合でレイトレジストをするプレイヤーは、たとえスキルのあるプレイヤーであっても上位TIER帯に入ることが難しくなることがわかる。
最後に、レイトレジストの度合いによる補正影響について、TIERレートが異なるプレイヤー別に示した。なお、対象プレイヤー以外のプレイヤーのTIERレートは全て初期値をとるものとする。
| 59left / 60entry | 49/60 | 39/60 | 29/60 | |
|---|---|---|---|---|
| -0.5 | -3.6 | -9.0 | -13.3 | |
| -0.5 | -3.6 | -9.0 | -13.3 | |
| -0.5 | -3.6 | -9.0 | -13.3 |
この表から、トーナメントの終盤になればなるほど、レイトレジストによる補正の影響を大きく受けることがわかる。また、レイトレジストの度合いが同じであれば、その補正の大きさは対象プレイヤーのTIERレートによらない。
まとめ
ここまで書いてきたように、TIERレーティングでは多くの要素をロジックに組み込んでおり一言で説明することは難しいが、ここに重要な点をまとめておく。
- TIERレーティングではプレイヤーのスキルが代表値 、分散 の正規分布に従うものとする。
- TIERレートが示す値は「プレイヤーの実力の最低保証ライン」である。
- の値は に対する信頼度と言い換えられ、トーナメントにエントリーすればするほどその値は収束し、TIERレートは上昇する。ただし、約15回エントリーで の値は下限値に達するため、それ以降は参加回数によるTIERレートへの寄与はなくなる。
- 既にBUSTしたプレイヤーがいる状態でレイトレジストをすると、トーナメントの終盤でエントリーすればするほど獲得TIERレートにマイナスの補正がかかり、トーナメントの序盤からプレイしているプレイヤーと比べて損をすることになる。ただし、リエントリー時においてのみレイトレジストに損得は発生しない。
- 推定ハンド数が少なければ少ないほど重要度の低い結果と見なされ、TIERレート変動幅は小さくなる。
- 順位にはICMの要素を強めるための傾斜がかけられており、1位になる/上位3%に入る/FT進出/下位3%から抜け出すことの重要度が高い。
- 対戦相手とのTIERレートが離れていればいるほど、対戦結果が想定通りであればTIERレートの変動率は小さく、想定通りでなければ大きくなる。
最後に
ここまでお読みいただきありがとうございます。
この記事では、ROOTS REWARDS Season.2において導入したTIERレーティングの仕組みやその設計思想について、さまざまな角度からご紹介しました。ポーカーの実力に即したレーティングシステムを作るためにはどうしたらいいかという点を徹底的に追求し、試行錯誤の末にリリースすることができたことを嬉しく思います。
ディレクターノートにもある通り、TIERレーティングという仕組みはポーカーの競技シーンという未来を作り出すために生まれました。「ランキング上位に挑戦する」「目の前のライバルを倒す」「同じ実力を持ったプレイヤー同士の勝負を楽しむ」など楽しみ方は人それぞれだと思いますが、そこにより多くの熱狂が生まれるのであれば嬉しい限りであり、開発者冥利に尽きます。
ぜひあなただけの目標を持って、新しいTIER MATCHに挑戦してみてください。
株式会社POKER ROOM
開発チーム
Works Cited
MicroSoft, et al. “TrueSkill(TM): A Bayesian Skill Rating System.” Ralf Herbrich,
https://www.microsoft.com/en-us/research/wp-content/uploads/2007/01/NIPS2006_0688.pdf. Accessed 25 November 2022.
“The Math Behind TrueSkill.” Moserware, 28 May 2011,
http://www.moserware.com/assets/computing-your-skill/The%20Math%20Behind%20TrueSkill.pdf. Accessed 25 November 2022.